在某些时候,我们知道观测数据是由某个概率模型产生的,但是我们不知道模型的参数。而通过观测数据估计模型参数就称为参数估计。参数估计有很多种方法:最大释然估计、最大后验估计、采样等。这篇文章主要讨论最大释然估计与最大后验证估计。
最大似然估计
在给定模型参数$ \theta $,观测到观测值 $X1$ 的概率为 $p(\mathbf{X}|\theta)$ ,这称之为似然函数。顾名思义,最大释然估计就是在已知观测值 $\mathbf{X}$ 的情况下估计$\theta$,使得 $p(\mathbf{X}|\theta)$ 最大。
举一个例子,抛一枚硬币 6 次,假设这枚硬币正面向上的概率为$\theta$,观测到的结果如下:
正 反 正 正 正 反
利用这个结果对 $\theta$ 进行一个估计。首先写出似然函数:
$$
p(\mathbf{X}|\theta)=(1-\theta)\theta^3(1-\theta)
$$
令导数为 0 ,求得 $\theta = \frac 2 3$。
有的同学看到这里嘴巴张成了 o 型。抛 6 次 4 次正面向上$\theta=\frac{2}{3}$,那抛 1 次正好有 1 次正面向上岂不是$\theta=1$?其实这里你已经开始使用 $\theta$ 的先验概率了。也就是说,在你以前的观察中,$\theta=0.5$的概率是最高的。而$\theta=1$是几乎不可能的。这也就是我们接下来要讲的最大后验估计。
最大后验估计
在上面提到,一般来说都会认为 $\theta=0.5$ 概率较大,而 $\theta=1$ 概率较小。这其实相当于我们认为 $\theta$ 也具有一个分布,例如正太分布。也就是将$\theta$看作一个随机变量。这里改变一下符号,令 $\Theta$ 表示需要估计的参数,而 $\theta$ 表示它一个具体的取值 。而最大后验估计的思想就是:
$$
\mathop{max}_\theta \ p(\Theta=\theta|\mathbf{X})
$$
也就是在观测到$\mathbf{X}$之后,估计$\Theta$并使得 $p(\Theta|\mathbf{X})$ 最大。利用贝叶斯公式:
$$
p(\Theta=\theta|\mathbf{X}) = \frac{p(\mathbf{X}|\Theta=\theta)P(\Theta=\theta)}{p(\mathbf{X})}
$$
这里的分母是一个常数,与 $\Theta$ 无关。于是我们只需要最大化分子就可以,于是最后为:
$$
\mathop{max}_\theta \ p(\mathbf{X}|\Theta=\theta)P(\Theta=\theta)
$$
可以看出,这里比最大释然估计多出了一个先验概率 $P(\Theta=\theta)$。
$$
p(\mathbf{X}|\Theta=\theta)
$$
例如这里我们假设$\Theta \backsim \it{N(0.5,0.1)}$。由于计算比较复杂,这里直接画出函数图像为:
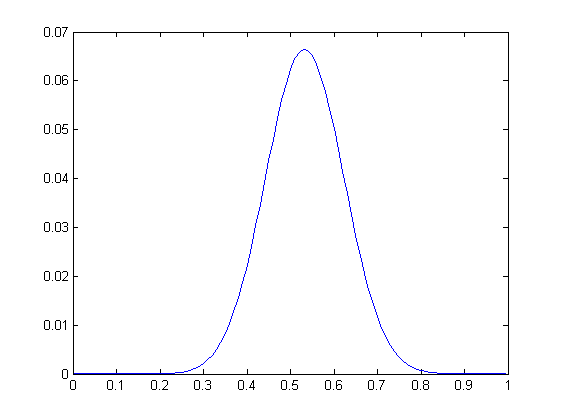
从图像可以估计出$\theta=0.55$,这个结果就比最大似然估计更加贴近实际。
总结
一般来说,在知道参数正确分布的时候,最大后验估计要优于最大释然估计。而最大似然估计与最大后验估计的差别用一句话概括为:
最大似然估计的估计量是一个未知常量,而最大后验估计的估计量是一个未知随机变量