异常检测-体验异常森林

Posted on   |   In

在异常检测-孤立森林中讲到了孤立森林的原理和详细算法。这篇文章主要是使用一下python 上的机器学习框架sklearn中的孤立森林模块，体验一下检测效果。

检测高斯分布数据

首先用产生1000个服从正太分布的数据,并画出散点图:

1
2
3
data = np.random.normal(50,10,(2000,2)) # 均值50 标准差10 1000个点
plt.scatter(data[:,0],data[:,1]) 
plt.show()

如下:

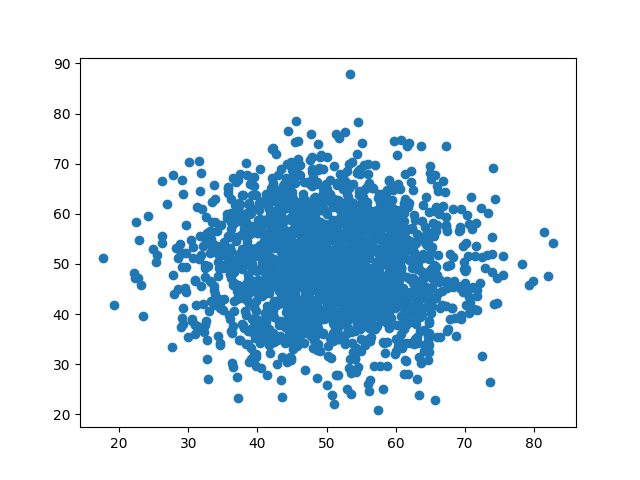
然后使用数据对孤立森林进行训练并获得异常得分:

1
2
3
4
from sklearn.ensemble import IsolationForest
forest = IsolationForest(n_jobs=4,n_estimators=100)
model =  forest.fit(data)
scores = 0.5 - model.decision_function(data)

注意 sklearn 异常得分对论文中的得分进行了一点转换，用0.5 - 实际得分 =最终得分。因此获得的得分可能为负值。这里再进行了一次处理转换回了符合原论文的形式，也就是得分为 [0-1]。在论文中提到，如果一个样本的得分接近与1,那么这个样本一定是异常点。但是论文中并没有给出明确的阈值来划分异常样本和正常样本。我们先看一下样本异常得分的分布图:

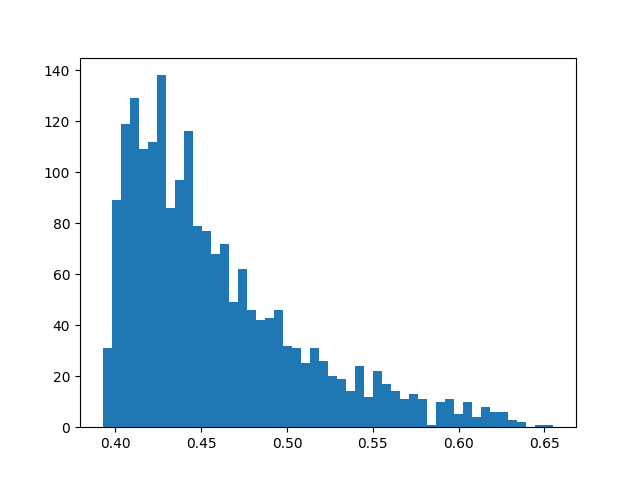
可以看出大部分的样本都在0.6以下，选择0.6作为阈值，用红点表示异常点:

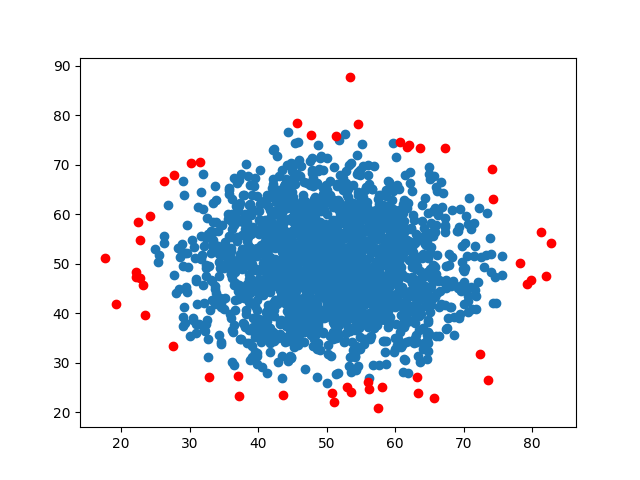
在边缘部分的点被检测为了异常点，这与我们利用概率模型进行检验的结果相同。但是由于是无监督训练，无法给出检测率和虚警率。

检测均匀分布数据

为了对比，我们需要对均匀分布的数据进行数据也进行一些分析。同样先产生样本:

1
2
3
data = np.random.uniform(0,100,(1000,2)) # 0-1000 均匀分布的1000个点
plt.scatter(data[:,0],data[:,1]) 
plt.show()

样本如下:

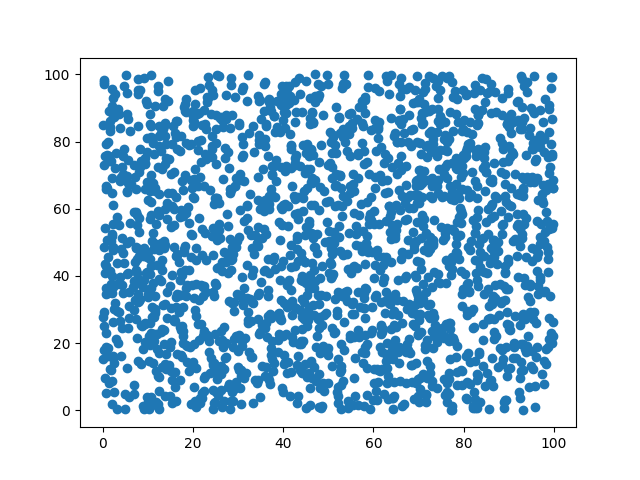
获取异常得分并画出得分分布直方图:

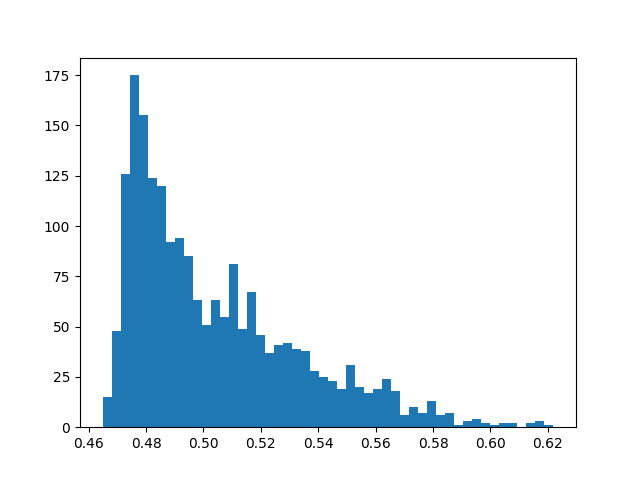
由于均匀分布产生的数据集应该没有明显的异常，这里就不对数据进行检测。而

结果对比

为了对比均匀分布的数据与正太分布数据的异常得分区别，利用同样的尺度画出分布曲线:

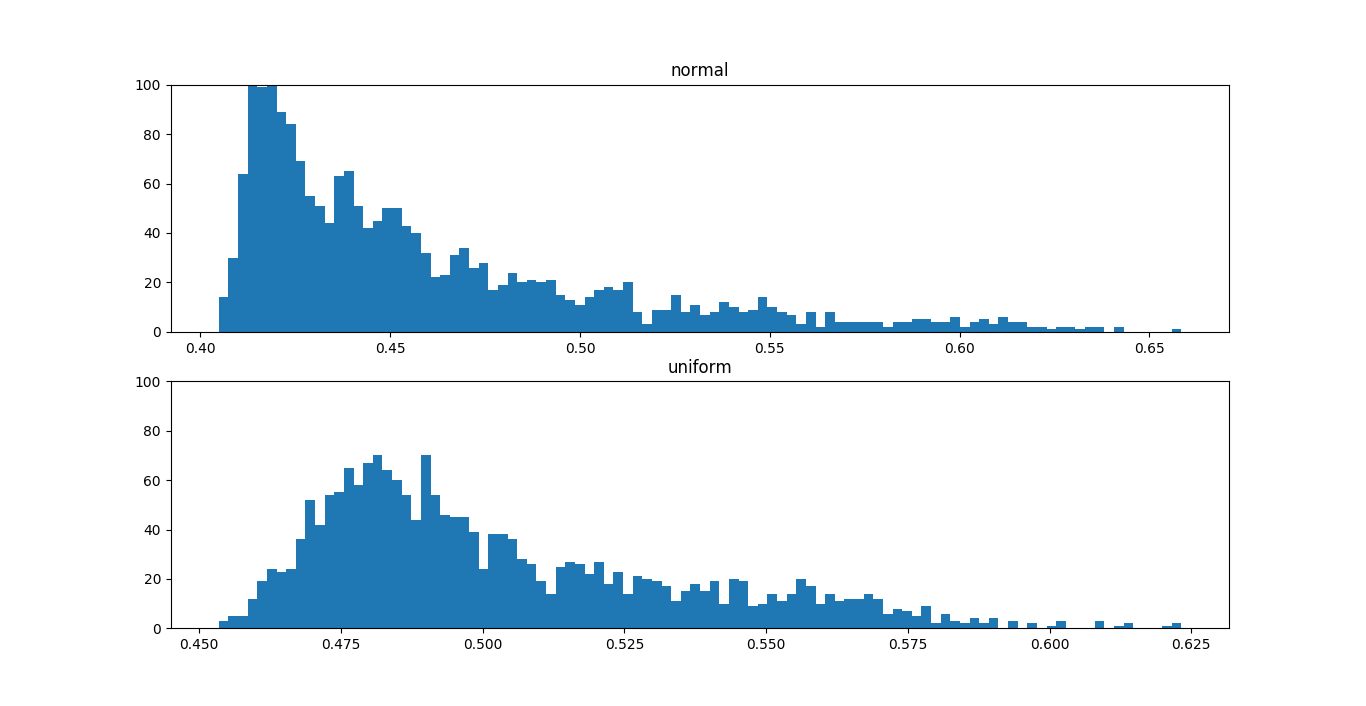
其中上图为正太分布频数直方图，下图为均匀分布频数直方图。

可以看出，正太分布的异常得分从低分到高分逐渐减少，类似与是一种长尾分布。这是可以理解的，因为最中心部分的元素最正常，得分也最低，然后边缘的样本异常得分逐渐增长。因此形成了这种左往右逐渐降低的分布。

从均匀分布的定义来看，样本出现在每一个位置的概率相同。但是由于采样误差和模型误差，导致样本的得分与理想情况不同。因此形成了一个类正太分布的情况。这也是比较合理的。为了证明这个猜想，我们手动生成一个完全理想的均匀分布数据如下:

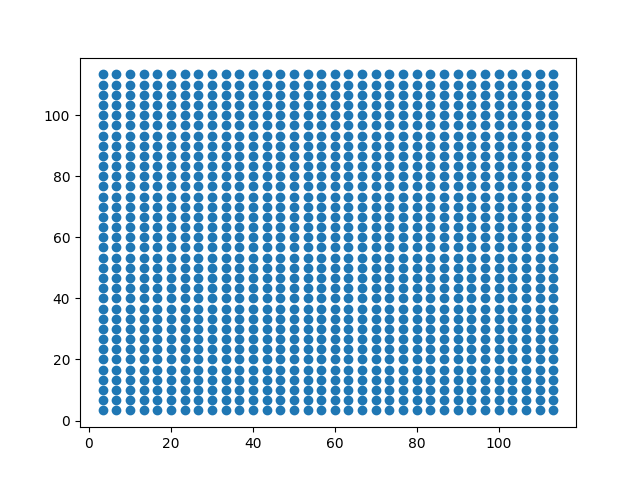
得到的频数分布为:

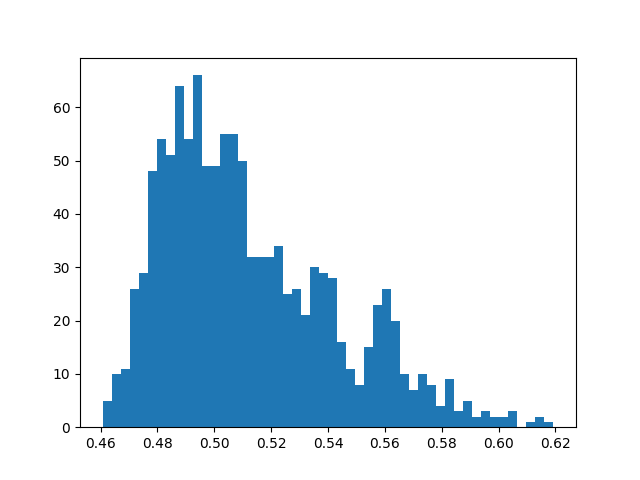
可以看出比不理想的均匀分布更作为训练数据时更接近于正太分布了。但是数据的结果仍然不够集中，因为理论上来说，均匀分布中每个样本的得分应该相同。所以异常得分频书分布应该是一条平行于y轴的直线，或者是方差非常小的正太分布图像。因此可以看出，至少在数据为均匀分布的情况，模型仍有较大误差。

总结与讨论

通过以上两个例子我们可以引出异常检测的一些难点与面临的问题:

  1. 由于需要已经异常检测的情况往往是无法获取到样本的标签，因此我们无法判断如何选取一个合适的阈值来将数据划分为正常数据和异常数据。
  2. 假如我们通过某种手段确定了一个阈值，将数据划分为正常、异常两部分。那么此时如何判断这个阈值的好坏？也就是说划分的异常样本是否据有参考价值？我们应该如何判断结果的可信度？
  3. 通过异常得分我们是否能够确定数据集中是否具有明显的异常样本？

总之一句话就是结论可信度的问题，我们无法判断模型在我们需要的数据集上的表现如何，当然这也不只是是孤立森林面临的问题。

此外，如果无法准确的判断每一个样本是否属于异常或正常情况。那么是否可以通过异常得分来判断某个数据集中总体异常水平？如果能判断，这也是一个非常有用的信息。